
Tipuri de costuri și comportamentul acestora (II)
Numărul 22, 12-18 iunie 2018 » Expertiza și auditul afacerilor
Termeni-cheie: costuri directe, costuri indirecte, cheltuieli fixe, cheltuieli variabile, capacitate de producție, grad de activitate, costul subactivității, cost marginal
Clasificare JEL: M41
Continuăm demersul făcut în numărul anterior al revistei cu prezentarea unor aspecte privind variabilitatea costurilor, procedeele de delimitare a cheltuielilor în variabile și fixe, capacitatea de producție și gradul de activitate, dar și costurile marginale.
4. Variabilitatea costurilor. Procedee (metode) de delimitare a cheltuielilor în variabile și fixe
În cazul cheltuielilor semivariabile sau al celor semifixe este importantă cunoașterea comportamentului acestora în vederea determinării unor algoritmi (procedee, metode) de delimitare a părții fixe, respectiv a celei variabile. În această categorie sunt incluse:
- procedeul celor mai mici pătrate (analiza regresiei);
- procedeul (metoda) punctelor de maxim și minim.
➜ Procedeul celor mai mici pătrate (analiza regresiei)
Prin analiza regresiei aflăm cheltuielile variabile unitare și cheltuielile fixe. Aceasta necesită parcurgerea următoarelor etape:
1. Calculul volumului mediu de activitate:
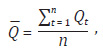
2. Calculul cheltuielilor medii:
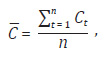
3. Calculul abaterii volumului activității din fiecare perioadă de gestiune luată în calcul față de volumul mediu al activității:
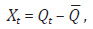
4. Calculul abaterii cheltuielilor din fiecare perioadă de gestiune luată în calcul față de media acestora:
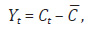
5. Calculul cheltuielilor variabile unitare:
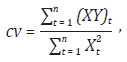
6. Calculul costurilor variabile totale aferente unei perioade de gestiune luate în calcul:
7. Calculul cheltuielilor fixe:
Cheltuielile fixe nefiind dependente de evoluția volumului activității, se vor efectua calcule pentru două perioade de gestiune oarecare.
8. Calculul cheltuielilor standard pentru o perioadă de gestiune viitoare:
➜ Procedeul (metoda) punctelor de maxim și minim
Utilizarea acestui procedeu implică parcurgerea următoarelor etape:
1. Calculul cheltuielilor variabile unitare:
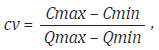
După determinarea cheltuielilor variabile unitare (cv), următoarele etape sunt similare cu etapele șase-opt prezentate în cadrul procedeului precedent.
Exemplu
În anul N-1, divizia Alfa din cadrul întreprinderii Beta înregistrează următoarele date privind numărul de ore-mașină și cheltuielile cu energia electrică:
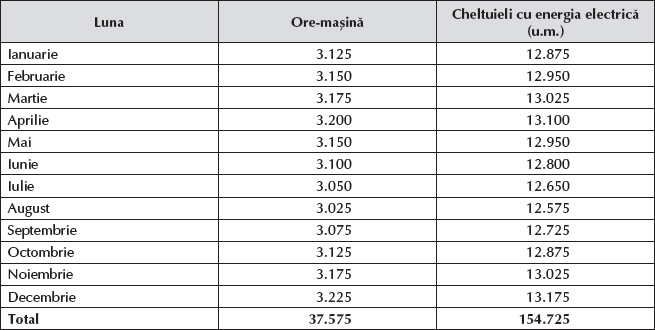
Ne propunem să determinăm cheltuielile standard estimate aferente energiei electrice din luna ianuarie N, în condițiile în care se preconizează funcționarea unui număr de 3.000 de ore-mașină, utilizând:
- procedeul celor mai mici pătrate (analiza regresiei);
- procedeul (metoda) punctelor de maxim și minim.
a) Procedeul celor mai mici pătrate (analiza regresiei)
Calculul volumului mediu de activitate:

Calculul cheltuielilor medii:

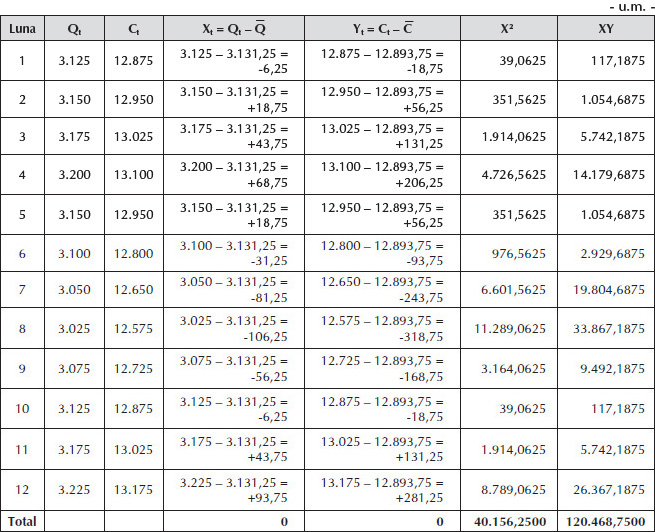
Determinarea cheltuielilor variabile unitare:
- Cheltuielile variabile unitare = Cheltuielile variabile/Oră-mașină = 120.468,75 u.m./40.156,25 ore-mașină = 3 u.m./oră-mașină
- Cheltuielile fixe aferente lunii august = 12.575 u.m. – (3.025 ore-mașină x 3 u.m./oră-mașină) = 3.500 u.m.
- Cheltuielile fixe aferente lunii decembrie = 13.175 u.m. – (3.225 ore-mașină x 3 u.m./oră-mașină) = 3.500 u.m.
Determinarea cheltuielilor standard pentru luna ianuarie N:
- Cheltuielile standard = 3.500 u.m. + (3.000 ore-mașină x 3 u.m./oră-mașină) = 12.500 u.m.
b) Procedeul (metoda) punctelor de maxim și minim
Calculăm cheltuielile variabile unitare aplicând formula:


Prin aplicarea formulei prezentate anterior, calculăm:
Costul variabil pe oră-mașină = 600 u.m./200 ore-mașină = 3 u.m./oră-mașină
Determinarea costurilor fixe:
Fiind constante, indiferent ce lună alegem pentru determinarea costurilor fixe, se obține aceeași valoare. Pentru exemplificare am luat în considerare două luni – august și decembrie:
- Costul fix pentru luna august = 12.575 u.m. – (3.025 ore-mașină x 3 u.m./oră-mașină) = 3.500 u.m.
- Costul fix pentru luna decembrie = 13.175 u.m. – (3.225 ore-mașină x 3 u.m./oră-mașină) = 3.500 u.m.
Determinarea costului standard pentru luna ianuarie N:
- Costul standard = 3.500 u.m. + (3.000 ore-mașină x 3 u.m./oră-mașină) = 12.500 u.m.
Astfel, indiferent de algoritmul de calcul aplicat (analiza regresiei sau metoda punctelor de maxim și minim), se obțin aceleași rezultate.
5. Delimitări conceptuale privind capacitatea de producție și gradul de activitate. Imputarea rațională a cheltuielilor fixe
În vederea analizei comportamentului costurilor variabile și al celor fixe este necesar să se prezinte informații despre capacitate, activitate și gradul de activitate, precum și analiza de detaliu a comportamentului costurilor totale și unitare. Potrivit Ebbeken et al. (2000, p. 62), capacitatea este definită de regulă ca fiind cantitatea maximă ce poate fi produsă într-o perioadă, măsurată după cum urmează:
- la întreprinderea cu producție unitară, omogenă: în tone, bucăți, metri cubi;
- la întreprinderea cu producție multiplă, eterogenă: ore de muncă sau ore de funcționare a mașinii.
În literatura de specialitate sunt întâlnite patru tipuri de capacitate de producție: teoretică (ideală), practică, suplimentară și normală.
✔ Capacitatea teoretică (ideală) – volumul maxim al producției finite pentru o perioadă dată de timp, în ipoteza că toate utilajele și echipamentele funcționează la viteza optimă fără întreruperi. Este utilă pentru estimarea nivelurilor maxime de producție, deși o întreprindere nu funcționează niciodată la capacitatea ideală.
✔ Capacitatea practică – capacitatea teoretică diminuată cu întreruperile normale și cu cele probabile ale activității. Acest mod de determinare este generat de faptul că producția este întreruptă din cauza defectării utilajelor sau pe perioadele necesare pentru reutilare, reparații curente și capitale și pauzele de lucru ale salariaților.
✔ Capacitatea suplimentară – surplusul de echipamente și utilaje menținute ca rezervă. Majoritatea întreprinderilor nu operează nici la capacitatea ideală, nici la cea practică, ci țin cont de capacitatea suplimentară. Aceste utilaje suplimentare sunt folosite atunci când cele obișnuite se află în reparație. Mai mult, pe perioadele cu activitate redusă, o societate poate folosi doar o parte din echipamentele sale sau poate lucra în unul ori două schimburi, în loc de 24 de ore.
✔ Capacitatea normală – nivelul mediu anual al capacității de producție necesar pentru a satisface cererea potențială de produse.
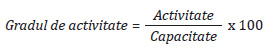
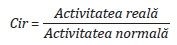
✔ Subactivitate – obținerea unui nivel al activității mai mic decât capacitatea normală de producție în cursul unei perioade. Conduce la înregistrarea unui cost al subactivității care se calculează astfel:
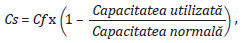
Aplicarea coeficientului de imputare rațională și determinarea unui cost al subactivității au un efect similar: diminuarea cu aceeași valoare a cheltuielilor fixe incluse în costul de producție.
✔ Supraactivitate – obținerea unui nivel al producției ce depășește capacitatea normală de producție.
Exemplu
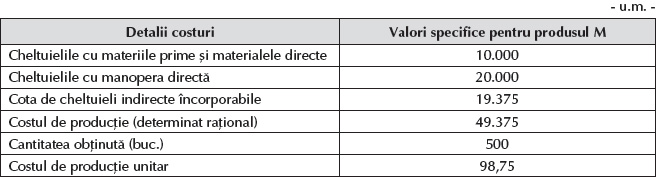
Întreprinderea Alfa obține într-o perioadă de gestiune un singur produs, M, și contabilizează:
- cheltuieli directe – 30.000 u.m., din care cheltuieli cu materiile prime și materialele consumabile– 10.000 u.m. și cheltuieli cu manopera directă – 20.000 u.m.;
- cheltuieli indirecte de producție – 20.000 u.m., din care cheltuieli fixe – 10.000 u.m.
Nivelul activității, exprimat în ore de funcționare rațională a utilajelor, este următorul:
- nivelul normal al activității – 8.000 de ore;
- nivelul real al activității – 7.500 de ore.
Cantitatea obținută din produsul M este de 500 de bucăți.
Ne propunem să calculăm costul subactivității, cheltuielile indirecte de producție și costul de producție unitar.
Cs = Cf x (1 – Capacitatea utilizată/Capacitatea normală) = 10.000 u.m. x (1 – 7.500 ore/8.000 ore) = 625 u.m.
6. Costurile marginale: definiție și aplicabilitate
Dat fiind că pe termen scurt variația costului total este identică din punct de vedere valoric cu variația costului variabil, costul total marginal este egal cu costul variabil marginal dacă sunt îndeplinite două condiții:
- menținerea unei structuri nemodificate la nivelul costurilor fixe;
- menținerea unei relații stricte de proporționalitate între costurile variabile și cantitatea obținută.
Exemplu
O întreprindere fabrică și comercializează 4 loturi de produse. Costul complet al acestora este de 1.200.000 u.m. Analiza evoluției costurilor arată că fabricarea a 5 loturi conduce la recunoașterea unui cost complet de 1.400.000 u.m.
Ne propunem să determinăm care este valoarea costului marginal generat de producția unui lot suplimentar.
Cmg = 1.400.000 u.m. – 1.200.000 u.m. = 200.000 u.m.
Potrivit Alazard și Sépari (2016, p. 202), în cazul în care funcția costului total este reprezentată printr-un model de curbă de forma literei „S”, costul marginal va fi o curbă de forma literei „U”:
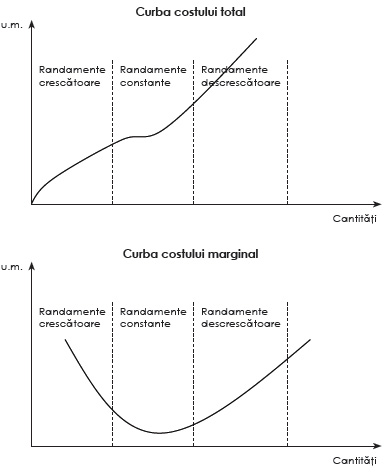
Pentru o structură dată este importantă cunoașterea cantității de produse pentru care costul mediu este minim, deoarece această cantitate permite o producție cu un cost scăzut.
Potrivit Alazard și Sépari (2016, p. 205), costul marginal este egal cu minimul costului mediu, punct cunoscut sub denumirea de optim tehnic (punctul A de pe grafic). Acesta exprimă cantitatea de produse pentru care combinația productivă este cea mai economică:
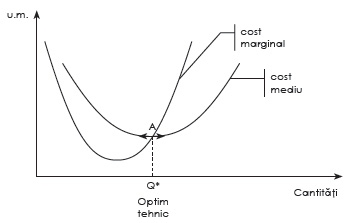
Profitul este maxim atunci când venitul marginal este egal cu costul marginal, punct cunoscut sub denumirea de optim economic. El reprezintă cantitatea pentru care eficiența economică este optimală.
Potrivit Alazard și Sépari (2016, p. 205), în cazul cel mai frecvent, în care prețul de vânzare descrește în funcție de cantitățile vândute, optimul economic (punctul B de pe grafic) poate fi prezentat astfel:
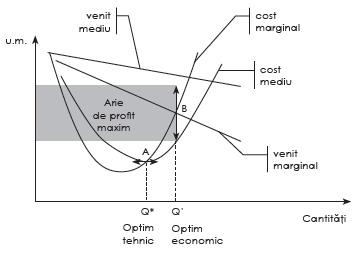
Aplicațiile costului marginal se regăsesc în cazul unei comenzi suplimentare. Toată comanda suplimentară este acceptată atâta timp cât acesta este inferior venitului marginal așteptat în urma comenzii.
Exemplu
O întreprindere lucrează la 80% din capacitatea sa de producție. Structura costurilor de producție pentru obținerea unei cantități de 8.000 de bucăți este următoarea:
- costuri variabile unitare – 1.000 u.m./buc.;
- costuri fixe (de structură) totale – 800.000 u.m.
Întreprinderea primește o comandă nouă de 1.000 de bucăți de produse realizate în condiții normale. Clientul acceptă să plătească pentru fiecare produs suma de 1.600 u.m.
- fiecare produs va trebui să suporte un tratament specific ce duce la majorarea costurilor variabile cu 10%;
- costurile fixe suplimentare se estimează la 100.000 u.m.?
a) Cele 1.000 de bucăți suplimentare nu vor acoperi capacitatea de producție de 10.000 de bucăți de produse, deci costul marginal va fi egal cu costurile variabile unitare. În acest caz avem:
- Costul marginal = 1.000 u.m./buc.
- Venitul marginal = 1.600 u.m./buc.
- Profitul obținut pentru o bucată (unitar) = 1.600 u.m./buc. – 1.000 u.m./buc. = 600 u.m./buc.
În acest context, rezultatul întreprinderii va crește cu 600.000 u.m. (600 u.m./buc. x 1.000 buc. (comanda clientului nou)). În consecință, întreprinderea va accepta prima comandă.
b) În acest caz, cererea este de 14.000 de bucăți (8.000 buc. + 1.000 buc. + 5.000 buc.), iar capacitatea de 10.000 de bucăți nu va fi suficientă pentru a face față cererii.
Pentru a analiza situația se va determina un cost marginal format din cheltuieli variabile unitare și se vor lua în considerare cheltuielile fixe suplimentare, necesare pentru extinderea capacității de producție, astfel:
- Cheltuielile variabile unitare = 1.000 u.m./buc. + (1.000 u.m./buc. x 10%) = 1.100 u.m./buc.
- Cheltuielile fixe suplimentare = 100.000 u.m.
Costul marginal va fi de 5.600.000 u.m. ((1.100 u.m./buc. x 5.000 buc.) + 100.000 u.m.), iar pentru un produs va fi de 1.120 u.m. (5.600.000 u.m./5.000 buc.). În consecință, va fi acceptat orice preț de vânzare mai mare decât costul marginal de 1.120 u.m.
BIBLIOGRAFIE
- Alazard, C., Sépari, S. (2016), Contrôle de gestion, ediția a IV-a, Dunod, Paris.
- Angelescu, C., Ciucur, D., Dinu, M. (2001), Dicționar de economie, Editura Economică, București.
- Ebbeken, K., Possler, L., Ristea, M. (2000), Calculația și managementul costurilor, Editura Teora, București.
- Needles, B.E. Jr., Anderson, H.R., Caldwell, J.C. (2001), Principiile de bază ale contabilității, ediția a V-a, traducere, Editura Arc, Chișinău.
Acest articol este preluat din lucrarea Contabilitate managerială, ediția a II-a, revizuită, autori Corina-Graziella Bâtcă-Dumitru, Daniela Artemisa Calu și Andreea Gabriela Ponorîcă, apărută la Editura CECCAR în anul 2018.
















Actuala „ofensivă” a cărții înregistrează noi victorii pe „frontul” lecturilor de calitate
Susținere financiară suplimentară pentru protejarea „Tezaurului Uman Viu”
ArtSafari: cinci expoziții de excepție cu opere ale marilor artiști plastici români
Istoria Teatrului, o „scenă” pentru eternitate
Cartea pentru copii, de la „Cenușăreasă” la podiumul premianților
Monumentele istorice, comori pentru eternitate
La MNAR, filmul de artă este la el acasă
România devine un hub cultural-artistic atestat și de un important festival cinematografic