Fundamentarea deciziilor de investiții cu ajutorul funcțiilor financiare din programele de calcul tabelar
Numărul 46-47, 27 nov. - 10 dec. 2018 » Expertiza și auditul afacerilor
Termeni-cheie: funcție financiară, valoare netă prezentă, rată internă de rentabilitate, cash flow, rată de actualizare, proiect de investiții
Clasificare JEL: G11, G12, G17, G19
1. Evaluarea investițiilor pe baza valorii nete prezente (NPV – net present value)
Funcția financiară NPV din Microsoft Excel arată valoarea netă prezentă a unei serii de cash flow-uri obținute anual în urma implementării unui proiect de investiții, ținând cont de valoarea acestora și de rata de actualizare, care este considerată a fi cel puțin egală cu rata dobânzii.
Pentru cash flow-urile obținute la intervale aleatorii de timp, în cadrul aceluiași exercițiu financiar sau în exerciții financiare diferite, dar succesive, se folosește funcția financiară XNPV.
Exemple
Prezentăm mai jos cum pot fi evaluate proiectele de investiții cu ajutorul funcțiilor financiare Excel NPV și XNPV.
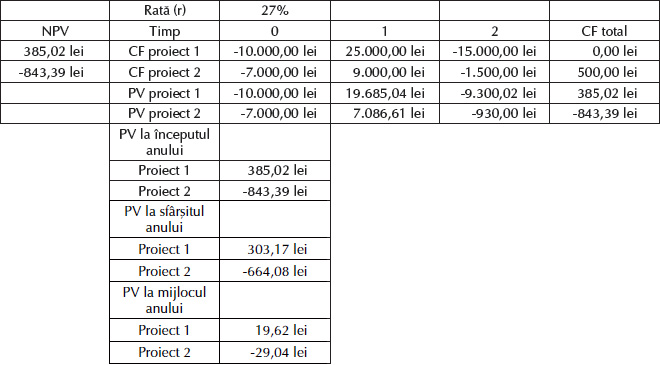
În Tabelul 1 am prezentat cash flow-urile generate în urma implementării a două proiecte de investiții. După cum se poate vedea, cash flow-urile sunt negative (outflows) în anul de bază, pozitive în anul 1 și din nou negative în anul 2. Cash flow-ul total este de 0 lei pentru investiția 1 și de 500 lei pentru investiția 2.
În mod rațional am alege proiectul 2, deoarece are un cash flow total mai mare decât proiectul 1. Însă, aplicând criteriul NPV, constatăm că valoarea netă prezentă (actualizată) a cash flow-urilor generate de proiectul 1 de investiții este de 385,02 lei, comparativ cu -843,39 lei pentru proiectul 2. Prin urmare, proiectul 1 este mai rentabil decât proiectul 2, care are o NPV negativă.
Pe liniile „PV proiect 1” și „PV proiect 2” am calculat valoarea actualizată a fiecărui cash flow în parte ținând cont de rata de actualizare de 27%, suma acestor valori reprezentând tocmai valoarea netă prezentă a fiecărui proiect.
De asemenea, am arătat că valorile actualizate diferă în funcție de momentul în care apar cash flow-urile: la începutul, la mijlocul sau la sfârșitul exercițiului financiar, cele mai mari valori fiind înregistrate la începutul anului pentru proiectul 1 și la mijlocul acestuia pentru proiectul 2 (deoarece are o NPV negativă).
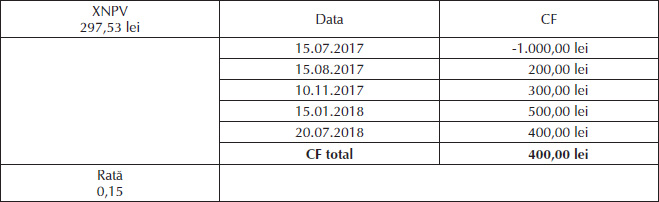
În Tabelul 2 am prezentat cash flow-urile generate de un proiect de investiții, care apar la momente aleatorii de timp din cadrul unui exercițiu financiar sau în exerciții financiare succesive.
Funcția financiară XNPV arată valoarea netă prezentă a acestor cash flow-uri, actualizate la o rată de 15%, care în cazul nostru este de 297,53 lei.
Formula de calcul a valorii nete prezente a unei serii de cash flow-uri pozitive sau negative este următoarea:
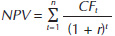
2. Evaluarea investițiilor pe baza ratei interne de rentabilitate (IRR – internal rate of return)
Funcția financiară IRR din Microsoft Excel determină rata de rentabilitate a unui proiect de investiții, care poate avea una sau mai multe rate de rentabilitate, sau chiar niciuna, în funcție de semnul plus sau minus al cash flow-urilor generate de investiția respectivă. De asemenea, funcția IRR calculează rata de rentabilitate a unei investiții ținând cont și de probabilitatea de apariție a cash flow-urilor generate de aceasta.
Exemple
Prezentăm mai jos cum pot fi evaluate proiectele de investiții cu ajutorul funcțiilor financiare Excel IRR și XIRR.
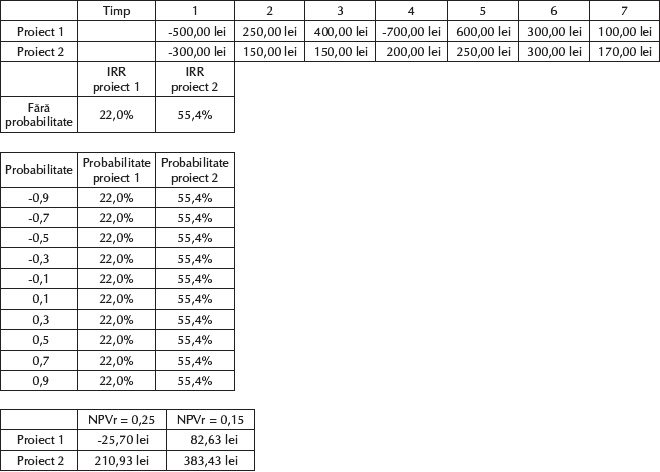
În Tabelul 3 am calculat rata internă de rentabilitate pentru două proiecte de investiții care generează cash flow-uri timp de 7 ani. Proiectul 1 are o rată de rentabilitate de 22%, iar proiectul 2, una de 55,4%, deci conform criteriului IRR este mai rentabil.
Se remarcă faptul că IRR se menține neschimbată chiar dacă variem probabilitatea de la -90% la 90%.
Proiectul 2 pare a fi mai rentabil decât proiectul 1 și din punctul de vedere al valorii nete prezente, calculată cu rate de actualizare de 25% și de 15%.
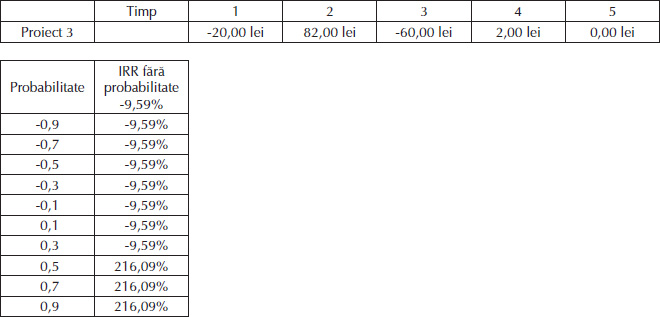
Proiectul 3, exemplificat în Tabelul 4, are o rată de rentabilitate negativă, de -9,59%, pentru probabilități cuprinse între -90% și 30%, și una pozitivă, de 216,09%, pentru probabilități de peste 50%. Totodată, se observă că acest proiect prezintă două rate de rentabilitate ca urmare a faptului că semnul +/– al cash flow-urilor generate de investiție variază de două ori pe parcursul celor 5 ani (cash flow-urile sunt negative în anii 1 și 3, pozitive în anii 2 și 4 și 0 în anul 5).
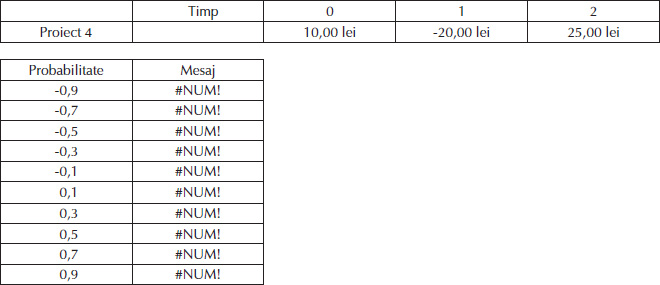
Proiectul 4, exemplificat în Tabelul 5, este genul de investiție pentru care nu se poate calcula o rată de rentabilitate, indiferent de probabilitatea de apariție a cash flow-urilor. Mesajul „#NUM!” pe care îl afișează Microsoft Excel în acest caz arată tocmai faptul că acest proiect nu are o rată de rentabilitate.

Tabelul 6 demonstrează că rata internă de rentabilitate nu este întotdeauna cel mai bun criteriu pentru alegerea unui proiect de investiții, deoarece nu ține cont de mărimea (scala) cash flow-urilor generate de acesta. Astfel, deși proiectul 2 prezintă o rată de rentabilitate superioară celei a proiectului 1 (IRR proiect 2 = 2,39; IRR proiect 1 = 1,35), valoarea netă prezentă a proiectului 1 (183,32 lei) este mult mai mare decât cea a proiectului 2 (3,41 lei). Aceasta deoarece cash flow-urile generate de investiția 1 sunt mai mari decât cele ale proiectului 2.
Prin urmare, deși aparent, conform IRR, proiectul 2 este mai rentabil decât proiectul 1, criteriul NPV scoate în evidență neajunsurile funcției IRR, respectiv faptul că aceasta nu ține cont de mărimea investiției, arătând că proiectul 1 este mai rentabil.
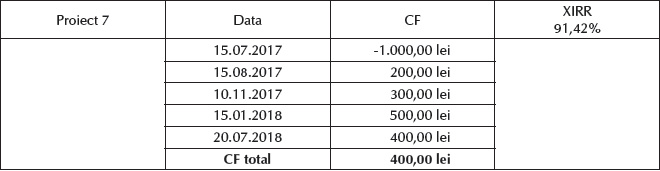
Ca și XNPV, funcția XIRR din Microsoft Excel calculează rata de rentabilitate a unui proiect de investiții care generează cash flow-uri la intervale aleatorii de timp. Astfel, proiectul 7, prezentat în Tabelul 7, are o rată internă de rentabilitate de 91,42%.
3. Funcțiile pentru decizii financiare personale
Funcțiile financiare PV (present value – valoarea prezentă), FV (future value – valoarea viitoare), PMT (payment – plata lunară), PPMT (principal payment – rata principală) și IPMT (interest payment– dobânda) ne ajută să aflăm valoarea prezentă sau viitoare a unei sume de bani de încasat ori de plătit, plata lunară aferentă unui credit, rata principală a creditului și dobânda.
Exemple

Presupunem că vrem să facem o investiție într-un mijloc fix și avem de ales între a plăti 16.000 lei acum sau câte 5.000 lei anual, pe o perioadă de 4 ani, la o dobândă constantă de 11% pe an.
În Tabelul 8 am folosit funcția PV pentru a calcula valoarea totală a plăților la începutul anului, la sfârșitul acestuia, precum și în cazul în care în ultimul an, pe lângă plata anuală de 5.000 lei trebuie să se achite o valoare reziduală de 700 lei.
Cu excepția plăților de la finalul anului, a căror valoare totală ajunge la 17.218,57 lei (> 16.000 lei), se dovedește mai avantajos să se achite pentru mijlocul fix câte 5.000 lei anual, timp de 4 ani, decât 16.000 lei în momentul de față (15.512,23 lei < 16.000 lei; 15.973,43 lei < 16.000 lei).
Semnul minus din fața sumelor arată că este vorba despre o plată, și nu despre o încasare.

Funcția financiară FV arată valoarea viitoare a unei sume de care dispunem în prezent sau a unei serii de plăți efectuate anual la o anumită rată a dobânzii, ținând cont și de valoarea unui depozit inițial.
În Tabelul 9 am folosit această funcție pentru a calcula valoarea viitoare a sumei de 5.000 lei plătite anual, la o rată anuală a dobânzii de 7%, pe o perioadă de 10 ani, în trei cazuri, și anume: i) plata se face la sfârșitul fiecărui an (valoarea depozitului peste 10 ani este de 69.082,24 lei); ii) plata se face la începutul fiecărui an (valoarea depozitului peste 10 ani este de 73.918 lei – mai mare decât în cazul precedent); iii) există un depozit inițial de 15.000 lei (valoarea depozitului peste 10 ani este de 103.425,27 lei).
Valorile obținute în exemplul de mai sus nu iau în considerare comisioanele bancare pentru deschiderea, gestionarea, lichidarea contului sau retragerea de numerar.
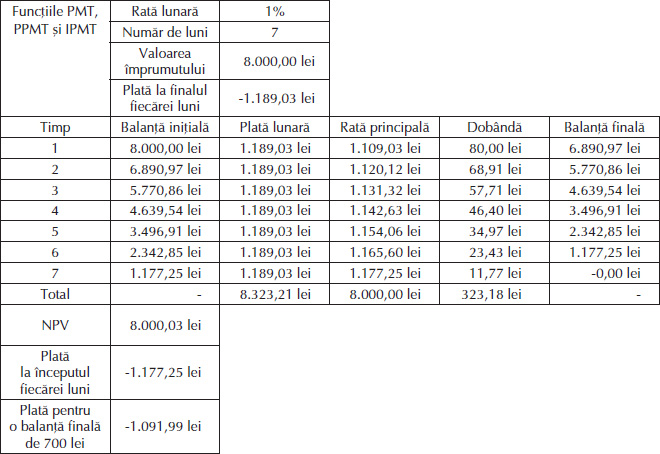
În Tabelul 10 am calculat cu ajutorul funcțiilor financiare PMT, PPMT și IPMT plata lunară, rata principală și dobânda pentru un împrumut de 8.000 lei, pe o perioadă de 7 luni, la o dobândă lunară de 1% (dobânda anuală este de 12%). În cazul în care plata se face la finalul fiecărei luni, se obține o valoare de 1.189,03 lei lunar, mai mare decât 1.177,25 lei, cât ar fi dacă plata s-ar face la începutul lunii.
Dacă vrem să avem o balanță finală de 700 lei, adică odată cu ultima rată să se plătească 700 lei pentru achitarea împrumutului, plata lunară se micșorează, ajungând la 1.091,99 lei (practic este ceea ce numim valoare reziduală în cazul unui contract de leasing).
Constatăm astfel că valoarea netă prezentă a celor 7 plăți lunare este de 8.000,03 lei, adică tocmai valoarea împrumutului. De asemenea, se remarcă faptul că, odată cu trecerea timpului, rata principală a împrumutului crește (de la 1.109,03 lei în prima lună la 1.177,25 lei în luna a șaptea), concomitent cu scăderea dobânzii (de la 80 lei în prima lună la 11,77 lei în luna a șaptea), plata lunară totală rămânând aceeași (1.189,03 lei).
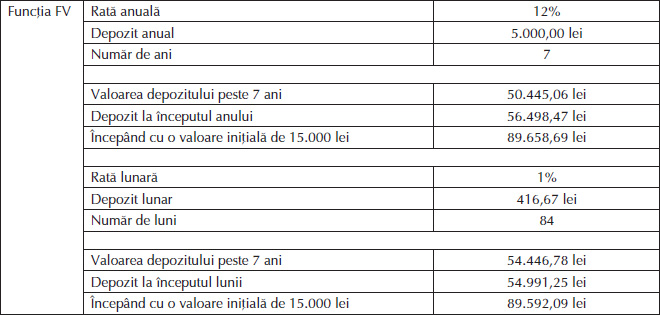
În Tabelul 11.a, pe baza funcției financiare FV, am realizat o comparație între un depozit anual de 5.000 lei cu o dobândă anuală de 12%, pe o perioadă de 7 ani, și același depozit, dar compus lunar, tot pe o perioadă de 7 ani (7 ani x 12 luni/an = 84 luni; dobânda lunară = 12% anual/12 luni = 1%; depozitul lunar = 5.000 lei anual/12 luni = 416,67 lei).
Se constată că după 7 ani valoarea este mai mare (54.446,78 lei > 50.445,06 lei) în cazul depozitului compus lunar, atunci când acesta se constituie la finalul fiecărei perioade, explicația fiind aceea că „dobânda la dobândă” apare de 12 ori mai mult în cazul depozitului compus lunar decât în al celui compus anual (84 de ori la depozitul lunar, față de 7 ori la cel anual).

În Tabelul 11.b am arătat avantajele compunerii lunare comparativ cu cea anuală. Deși valoarea depozitului (5.000 lei), rata anuală a dobânzii (12%) și perioada (5 ani) sunt aceleași în ambele cazuri, peste 5 ani valoarea depozitului compus lunar este mai mare decât în cazul compunerii anuale (9.083,48 lei > 8.811,71 lei), deoarece capitalizarea dobânzii se face de 12 ori mai des (de 60 de ori la depozitul lunar, față de 5 ori la cel anual). Altfel spus, pentru aceeași sumă, aceeași perioadă de timp și aceeași rată a dobânzii, câștigăm mai multă „dobândă la dobândă” în cazul compunerii lunare comparativ cu cea anuală.
Un alt avantaj al compunerii lunare este faptul că depozitul poate fi modificat (mărit, micșorat sau retras) după fiecare lună fără să se piardă dobânda aferentă acesteia, pe când depozitul compus anual nu poate fi modificat o perioadă de 12 luni.
Prin urmare, deși unele bănci afișează uneori o dobândă anuală mai mică în cazul depozitelor compuse lunar decât pentru cele anuale (de exemplu, 0,85% pentru depozitele constituite pe o lună și 1,70% – deci dublu – pentru cele constituite pe un an), este posibil ca cele dintâi să fie totuși mai avantajoase.
Concluzii
Funcțiile financiare ale programului de calcul tabelar Microsoft Excel sunt utile în analiza și modelarea datelor deoarece ne scutesc de calculele clasice, în care, modificând o singură cifră, trebuie refăcute toate socotelile. În Excel, dacă se schimbă unul sau mai multe elemente, toate calculele se refac imediat, în mod automat, pe bază de formule și/sau funcții.
Funcțiile financiare ale programelor de calcul tabelar pot veni în completarea altor module sau programe informatice de analiză și diagnostic financiar-contabil, inclusiv pentru realizarea de trenduri și previziuni financiare.
BIBLIOGRAFIE
- DeFusco, Richard A., McLeavey, Dennis W., Pinto, Jerald E., Runkle, David E. (2004), Quantitative Methods for Investment Analysis, ediția a II-a, CFA Institute.
- Dumitrean, Ioan (2010), Valori folosite în evaluarea de bunuri, acțiuni, societăți sau afaceri, Tribuna Economică, nr. 6/iunie.
- Dumitrean, Ioan (2012), Influența timpului asupra evaluării afacerilor. Analiză. Diagnostic. Evaluare, Editura Universității „Alexandru Ioan Cuza”, Iași.
- Dumitrean, Ioan (2018), Care tranzacție este mai avantajoasă: cash, credit sau leasing?, Contabilitatea, expertiza și auditul afacerilor, nr. 5/mai.
- Needles, Belverd E., Jr., Anderson, Henry R., Caldwell, James C. (2000), Principiile de bază ale contabilității, ediția a V-a, Editura Arc, Chișinău.
- Peterson Drake, Pamela, Fabozzi, Frank J. (2009), Foundations and Applications of the Time Value of Money, John Wiley & Sons.
- Stowe, John D., Robinson, Thomas R., Pinto, Jerald E., McLeavey, Dennis W. (2002), Analysis of Equity Investments: Valuation, United Book Press.
- Vance, David E. (2003), Financial Analysis & Decision Making. Tools and Techniques to Solve Financial Problems and Make Effective Business Decisions, McGraw-Hill.














Litoralul, o imensă scenă a artei de calitate
Cultură și statistică. Drumul spre mai mult și mai bine
Sub egida Ateneului Român, o vară muzicală de excepție
Expoziție la BNR: „Un alt fel de tezaur: Campionii României”
Bookfest 2024, încă un pas al editurilor spre armonizarea ofertei cu cererea
Festivalul Internațional Shakespeare. Din nou, Craiova la superlativ
Festivalul Filmului European. A șaptea artă, la superlativ
„Fără cărți, istoria e tăcută, literatura nu are glas, știința e infirmă, iar gândirea suspendată”